🔬 Integrated Rate Laws: Understand Reactions Over Time

Integrated rate laws help explain how reactant concentrations change with time. They are essential in chemical kinetics for predicting reaction durations, remaining reactants, and determining reaction order.

🎯 Why Are Integrated Rate Laws Important?

• Predict how long a reaction will take
• Calculate how much reactant remains at any time
• Determine the reaction order
• Calculate half-life (time for half the reactant to disappear)

🔢 Types of Integrated Rate Laws

🟦 Zero-Order Reaction

Rate is independent of concentration.

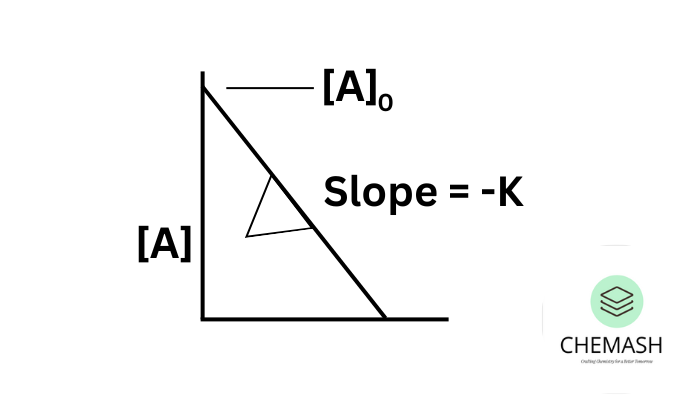
Equation: [A] = [A]₀ − kt

• Graph: [A] vs. time → straight line (slope = -k)
• Half-life: t_1/2 = [A]₀ / 2k
• Example: Degradation of drugs at a constant rate

🟩 First-Order Reaction

Rate depends linearly on concentration.

Equations: [A] = [A]₀e^−kt or ln[A] = ln[A]₀ − kt

• Graph: ln[A] vs. time → straight line (slope = -k)
• Half-life: t_1/2 = 0.693 / k (constant!)
• Examples: Radioactive decay, drug metabolism

🟥 Second-Order Reaction

Rate depends on the square of the concentration.

Equation: 1/[A] = 1/[A]₀ + kt

• Graph: 1/[A] vs. time → straight line (slope = k)
• Half-life: t_1/2 = 1 / (k[A]₀)
• Examples: Some organic reactions and dimerizations

🧠 Summary Table of Integrated Rate Laws

Order	Graph (Linear)	Half-life	Depends on [A]0?
Zero	[A] vs. t	t₁/₂ = [A]0 / 2k	Yes
First	ln[A] vs. t	t₁/₂ = 0.693 / k	No
Second	1/[A] vs. t	t₁/₂ = 1 / (k[A]0)	Yes

🚀 Real-World Use Case

When taking medication, doctors often use first-order rate laws to determine dosage timing and drug clearance. This helps ensure that drug levels stay effective without being toxic.