Mass Defect & Binding Energy
In nuclear chemistry, two fundamental ideas—mass defect and binding energy—play a major role in explaining atomic stability and nuclear energy. These concepts reveal why nuclei remain intact and how nuclear reactions release tremendous energy.
What is Mass Defect?
When scientists calculate the total mass of individual protons and neutrons in a nucleus, the result always turns out to be slightly more than the actual nuclear mass. This difference is known as the mass defect.
Mass Defect (Δm) = [Z × mass of proton + N × mass of neutron] – Actual mass of nucleus
Where:
• Z = Number of protons
• N = Number of neutrons
In other words, some mass appears to be “missing.” However, that mass doesn’t disappear. Instead, the nucleus converts it into energy that holds it together. This leads us to the concept of binding energy.
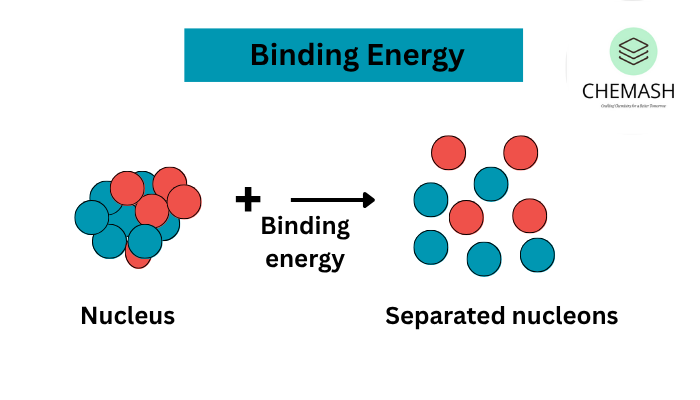
What is Binding Energy?
Binding energy refers to the energy required to separate a nucleus into its individual protons and neutrons. Conversely, this energy also gets released when nucleons come together to form a nucleus. Therefore, binding energy is what keeps the nucleus stable.
Einstein’s famous equation expresses the relationship between mass and energy:
E = Δmc²
Where:
• E = Binding energy (in joules)
• Δm = Mass defect (in kg)
• c = Speed of light (3 × 10⁸ m/s)
In nuclear chemistry, we usually express binding energy in MeV (Mega electron volts). For convenience, you can use this conversion:
1 atomic mass unit (u) = 931.5 MeV of binding energy.
Example: Helium-4 Nucleus
Let’s explore the concept of mass defect and binding energy using the Helium-4 nucleus, which contains 2 protons and 2 neutrons.
- Mass of 2 protons = 2 × 1.007276 u = 2.014552 u
- Mass of 2 neutrons = 2 × 1.008665 u = 2.017330 u
- Total expected mass = 4.031882 u
- Actual nuclear mass = 4.002603 u
- Mass defect = 0.029279 u
- Binding energy = 0.029279 × 931.5 = 27.3 MeV
As a result, 27.3 MeV of energy becomes available when the Helium-4 nucleus forms. To break the nucleus, the same amount of energy would be needed.
Binding Energy per Nucleon
The binding energy per nucleon tells us how tightly each proton or neutron is bound in a nucleus. It serves as a helpful indicator of nuclear stability.
Binding Energy per Nucleon = Total Binding Energy / Total Number of Nucleons
• Nuclei with higher binding energy per nucleon, such as Iron-56, show greater stability.
• In both fission and fusion, energy gets released as the products usually have a higher average binding energy.
Importance in Nuclear Reactions
- In Fission: A heavy nucleus splits into smaller, more stable ones. Consequently, energy is released.
- In Fusion: Two light nuclei merge to form a heavier nucleus with higher binding energy per nucleon, releasing energy.
- Nuclear Stability: Greater binding energy directly translates to increased nuclear stability.
✅ In conclusion, mass defect and binding energy reveal the true source of nuclear energy and explain atomic stability.
