Speed and Velocity — Class 9/10 Physics
Speed and velocity are two important quantities used to describe the motion of an object. Although they seem similar in daily life, in Physics they are different in meaning and calculation. This chapter explains their definitions, formulas, key differences, and example questions.
What is Speed?
Speed is the distance covered by an object in unit time. It tells us how fast an object is moving but does not tell the direction of motion.
Formula:
Speed = Distance / Time
- Speed is always positive
- It does not depend on direction
- It is a scalar quantity
What is Velocity?
Velocity is the displacement of an object in unit time. It tells us both speed and direction of motion.
Formula:
Velocity = Displacement / Time
- Velocity depends on direction
- It can be positive, negative, or zero
- It is a vector quantity
Example:
If a car moves 40 m east in 5 seconds:
Velocity = 40 ÷ 5 = 8 m/s (towards east)
Average Speed
Average speed is the total distance traveled divided by the total time taken.
Formula:
Average Speed = Total Distance / Total Time
- Always positive
- Does not consider direction
- Scalar quantity
Example:
If a person runs 2 km and walks 1 km in 1 hour total:
Average Speed = 3 km / 1 hr = 3 km/h
Average Velocity
Average velocity is the total displacement divided by the total time taken.
Formula:
Average Velocity = Δx / Δt = (x₂ − x₁) / (t₂ − t₁)
- Vector quantity
- Direction indicated by sign (+ or −)
- Can be zero even if distance is non-zero
Example:
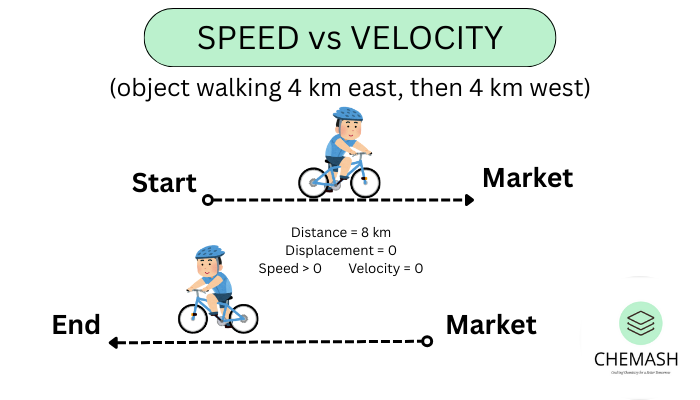
A person goes 4 km east and returns 4 km west to the starting point in 2 hours:
Displacement = 0 → Average Velocity = 0 / 2 = 0 km/h
Instantaneous Velocity
Instantaneous velocity is the velocity of an object at a particular moment in time.
Formula (Derivative form):
v = dx/dt
- Found using the tangent to the position–time graph
- Shows the exact speed and direction at that instant
Instantaneous Speed
Instantaneous speed is the magnitude of instantaneous velocity.
- Always positive
- Scalar quantity
Difference Between Speed and Velocity (Table)
| Feature | Speed | Velocity |
|---|---|---|
| Meaning | Rate of distance covered | Rate of displacement |
| Formula | Distance / Time | Displacement / Time |
| Quantity Type | Scalar | Vector |
| Value | Always positive | Can be +, − or 0 |
| Direction | Not considered | Direction considered |
Numerical Example
A cyclist travels 4 km north and 3 km south in 70 minutes.
- Total distance = 4 + 3 = 7 km
- Displacement = 4 − 3 = 1 km north
Average Speed = 7 km / 70 min = 0.1 km/min
Average Velocity = 1 km / 70 min ≈ 0.014 km/min north
MCQs — Practice Questions
- Which of the following is a vector?
(a) Speed (b) Distance (c) Velocity (d) Time
Answer: (c) - Average velocity becomes zero when:
(a) Time is zero (b) Displacement is zero (c) Distance is zero (d) Speed is zero
Answer: (b) - Instantaneous velocity refers to:
(a) Velocity at any time interval (b) Velocity at a specific instant (c) Average speed (d) Maximum speed
Answer: (b)
Quick Quiz for Students
- If a car moves in a circle and returns to the starting point, what is its displacement?
- Can speed be zero while velocity is non-zero?
- If distance = displacement, what does it mean about the path taken?
Conclusion
Speeds and velocity are related but different. Speed only tells how fast an object is moving, while velocity tells both speed and direction. Average speed depends on total distance, whereas average velocity depends on displacement. Instantaneous values describe motion at a specific moment.
NCERT Official Physics Resources
